Huffman Coding

Over at Harder, Better, Faster, Stronger, Steven Pigeon has a nice post on Huffman codes. He explains how Huffman codes operate and works through a pencil and paper example. Because he doesn’t give a real implementation and because the usual implementation uses a priority queue, I’d like to continue his discussion here. Take a minute to read Pigeon’s post so that you can more easily follow along.

Once you have the priority queue, the rest is pretty simple. Following the original post, we’ll build the Huffman code for the symbols a, b, c, d, and e with frequencies 3, 3, 2, 1, 1 respectively. We encode that as

(define nodes '((b . 3) (a . 3) (c . 2) (d . 1) (e . 1)))

I switched the order of the a and b nodes so that I get the same tree as he does instead of the equivalent tree with the roles of a and b reversed. Here’s the code to build the Huffman tree:

 1:  (define huffman
 2:    (lambda (nodes)
 3:      (define less?
 4:        (lambda (a b)
 5:          (< (cdr a) (cdr b))))
 6:      (let ((q (make-heap (length nodes) less?)))
 7:        (for-each (lambda (n) (q 'push n)) nodes)
 8:        (let loop ((right (q 'pop)) (left (q 'pop)))
 9:          (if (not left)
10:              (car right)
11:              (begin
12:                (q 'push (cons (list (car left) (car right))
13:                               (+ (cdr left) (cdr right))))
14:                (loop (q 'pop) (q 'pop))))))))

Lines 3–5 define the comparison function less?, and lines 6 and 7 make and fill the priority queue. The actual building of the tree is on lines 8–14. Just as explained in Pigeon’s post, the two nodes with the lowest frequencies are popped off the queue and replaced by a new node that combines them. This is repeated until the queue has only one entry and then that entry is returned. When we run this with nodes we get

((a b) (c (d e)))

which is the tree

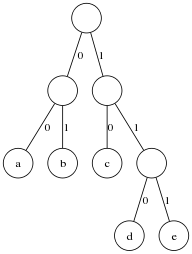
where I’ve labeled the left edges 0 and the right edges 1. You can easily read off the codes for a, b, c, d, and e from the tree. Here is the code to do it programnatically:

(define print-codes
  (lambda (tree)
    (define walk
      (lambda (code tree)
        (if (not (pair? tree))
            (format #t "~s ~s\n" tree (reverse code))
            (begin
              (walk (cons 0 code) (car tree))
              (walk (cons 1 code) (cadr tree))))))
    (walk '(0) (car tree))
    (walk '(1) (cadr tree))))

As you can see, it does a depth-first search of the tree recording its path as it goes. When it reaches a leaf node, it prints the name of the node and its path. Running it on the tree ((a b) (c (d e))) yields

a (0 0)
b (0 1)
c (1 0)
d (1 1 0)
e (1 1 1)

Decoding is similar to print-codes:

(define decode
  (lambda (msg tree)
    (define walk
      (lambda (msg tree)
        (cond
         ((not (pair? tree)) (cons msg tree))
         ((zero? (car msg)) (walk (cdr msg) (car tree)))
         (else (walk (cdr msg) (cadr tree))))))
    (let ((symbol (walk msg tree)))
      (format #t "~s " (cdr symbol))
      (if (not (null? (car symbol)))
          (decode (car symbol) tree)
          (newline)))))

It walks the tree guided by the message’s zeroes and ones. When it reaches a leaf, it prints the leaf’s name and starts over with the rest of the message.

There’s no requirement, of course, that the symbol be a single character. If we run huffman as

(huffman '((to . 2) (be . 2) (or . 1) (not . 1)))

we get the tree

((be (or not)) to)

and the codes

be (0 0)
or (0 1 0)
not (0 1 1)
to (1)

and can then encode “to be or not to be” as 1 0 0 0 1 0 0 1 1 1 0 0.