I’ve mentioned Atabey Kaygun’s blog before. He mostly writes short posts on some mathematical algorithm, which he illustrates with Lisp. One such post was about generating random trees of \(n\) nodes in such a way that every possible tree having \(n\) nodes is equally likely.
This turns out to be ridiculously easy and a simple induction shows that each tree is, in fact, equally likely. See Atabey’s post for the details of the proof. The idea of the algorithm—as well as the proof—is that given a random tree of \(n-1\) nodes, we randomly chose one of those \(n-1\) nodes and make the new, \(n^{\textrm{th}}\), node a child of that random node. Here’s the algorithm in Elisp:
(defun make-random-tree (nodes) (let (tree) (do ((n 1 (1+ n))) ((= n nodes) (reverse tree)) (push (list (random n) n) tree)))) (make-random-tree nodes)
Running the algorithm with \(nodes=6\) yields the pairs
| 0 | 1 |
| 0 | 2 |
| 1 | 3 |
| 0 | 4 |
| 4 | 5 |
where the pair \((x, y)\) means that \(y\) is a child of \(x\). The tree generated from the above is:
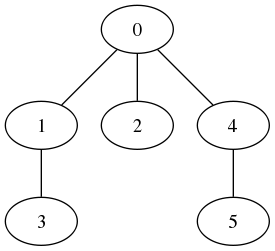
I’m writing about this for two reasons. First, obviously, it’s a neat result and potentially useful. Imagine, for example, that you have an algorithm that operates on trees and you want to generate test cases. This simple algorithms is all you need.
Second, writing it indulges my love for reproducible research. The Elisp code for generating random trees is run right in the buffer and it’s output automatically inserted into the buffer. Then other code (in the buffer but not exported) is run to draw the tree. The Org-mode source for this post could be considered a post generator. Every time I run it, I get a slightly different post.
Emacs and Org are so useful for this sort of thing that I consider it a cache miss if I have to do any processing outside of Emacs when I’m writing up results that involve calculations or other processing on data.
