References to Jeremy Kun’s The Mathematics of Secret Sharing keep popping up in my feed so it appears there’s some interest in it. The problem is to entrust shares in a secret to \(n\) people in such a way that the secret can be recovered if \(k\) shareholders \((k < n)\) agree to reveal the secret. If less than \(k\) of the shareholders agree, the secret remains hidden. For each shared secret, the number \(k\) is fixed but any number of shares can be distributed. The secret must be a number so in practice the secret will usually be an encryption key.
It might seem like this would be a difficult problem requiring some esoteric mathematics but it turns out to be simple and requires no more than high school mathematics. The method uses the fact that it takes \(m + 1\) points to recover an \(m^{\textrm{th}}\) degree polynomial (because, after all, there are \(m + 1\) coefficients to determine). For example two points determine a line (1st degree polynomial), three points determine a parabola (2nd degree polynomial) and so on.
As an example, suppose our secret is 7, that we want 6 shareholders, and that we require at least 4 shares to reveal it. We define a third degree polynomial with a constant term of 7, say \(x^{3} + 3x^{2} – x + 7\), and then pick 6 points on the polynomial (avoiding the \(x=0\) point) and give each of the shareholders a point. This is illustrated in Figure 1 where the green points are given to the shareholders and the blue point corresponds to the secret.
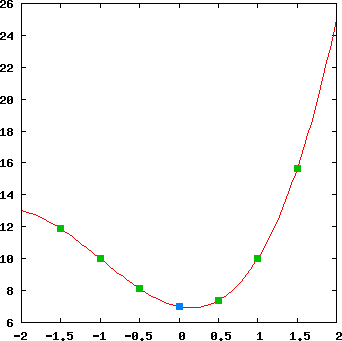
Figure 1: \(x^{3} + 3x^{2} – x + 7\)
Now if four of the shareholders agree to reveal their points, it is a simple matter to recover the polynomial with Lagrangian interpolation1, and retrieve the secret as the constant term.
This method has the advantage of being theoretically unbreakable. If an attacker has \(j < k\) points, a polynomial having any desired constant term can easily be constructed that passes through the \(j\) points. That means that the \(j\) points could represent any secret. Only by having \(k\) points can an attacker recover the secret.
For various technical reasons the calculations should be carried out over a finite field. That doesn’t really change anything except that “division” calculations are a bit more difficult. Tomorrow, I’ll present Lisp code that implements Shamir’s Secret Sharing over the finite field \(\mathbb{Z}_{p}\) where \(p\) is a 256 bit prime.
Footnotes:
Rather than computing the actual polynomial, we can recover the constant term directly with \[\sum_{j=0}^{k-1} y_{j} \prod_{\substack{0\leq{}m\leq{}k-1 \\ m\neq{}j}} \frac{-x_{m}}{x_{j}-x_{m}}\] where \((x_{0}, y_{0}) \ldots (x_{k-1}, y_{k-1})\) are the \(k\) points required for a \((k-1)^{\textrm{st}}\) degree polynomial. All that’s going on here is that we’re evaluating the Lagrange polynomial at 0.
We could also solve the four simultaneous equations by hand or use the Vandermonde matrix and Guassian elimination.
