I ran across an interesting interview question the other day: Given a base word and a list of other words, use the Levenshtein distance to find the social network of the base word in the list of other words. More specifically, we call wordb a friend of worda if the Levenshtein distance between them is 1. The problem is to start with the base word, find all its friends in the other list, then find all the friends of the friends, and so on. This problem is representative of a large class of related problems (such as The Six Degrees of Kevin Bacon) so it’s worthwhile considering how to solve it.
The Wikipedia article on Levenshtein distance has a straightforward pseudocode implementation of an algorithm to find the Levenshtein distance between two words that I translated directly into Lisp. I won’t bother showing the code since it’s pretty much a one-to-one translation.
The basic strategy is to do a breadth-first search of the base word’s social graph. We don’t have the graph, of course, that’s what we want to find. Instead, we build it up piece by piece. The main tool for doing breadth-first searches is a queue or FIFO. I’ve disussed these and given an implementation before. The implementation at the link is in Scheme but it’s trivial to convert it to Common Lisp. Again, I won’t bother showing the Lisp implementation.
With those two pieces in place, it’s pretty easy to implement the algorithm to find the social network.
1: (defun social (word words &optional graph) 2: "Find the social graph for word in the population words" 3: (let ((inside (make-instance 'queue)) 4: (outside (make-instance 'queue :initial-contents words)) 5: (new-outside (make-instance 'queue)) 6: (results (list (cons word 0))) 7: nodes) 8: (pushq (cons word 0) inside) 9: (do ((datum (popq inside) (popq inside))) 10: ((null datum) (if graph (sgraph (reverse nodes)) (reverse results))) 11: (destructuring-bind (word . distance) datum 12: (do ((potential-friend (popq outside) (popq outside))) 13: ((null potential-friend)) 14: (if (= (levenshtein word potential-friend) 1) 15: (let ((friend (cons potential-friend (1+ distance)))) 16: (pushq friend inside) 17: (push friend results) 18: (push (cons (car datum) potential-friend) nodes)) 19: (pushq potential-friend new-outside)))) 20: (rotatef new-outside outside))))
The implementation uses 3 queues:
- The
outsidequeue that holds words that have not yet been identified as friends. It’s initial value is the list of other words. - The
insidequeue that holds friends that are waiting to be processed. It is initialized to the base word with a distance (from the base word) of zero at line 8. - The
new-outsidequeue that holds words from theoutsidequeue that aren’t friends of head of theinsidequeue.
The main loop pops off the head of the inside queue at line 9 and checks each word on the outside queue to see if it is a friend. If it is, it adds that word and its distance from the base word to the end of the inside queue (line 16), it adds the same to the results list (line 17), and finally adds the two words being compared onto the nodes list (line 18). If the word being checked is not a friend, it is pushed onto the end of the new-outside queue.
When the outside queue is empty, it is swapped with new-outside and the main loop starts over. When the inside queue goes empty, the process is complete. Assuming graph is NIL, the results are returned.
If *words* is given by
(defparameter *words* '("milk" "silk" "mill" "mails" "mills" "miles" "silly" "smiles" "smile" "mile" "sill" "hilly" "shill" "mall" "bill" "bull"))
and the base word is bilk, the results of a run are:
SOCIAL> (social "bilk" *words* ) (("bilk" . 0) ("milk" . 1) ("silk" . 1) ("bill" . 1) ("mill" . 2) ("mile" . 2) ("sill" . 2) ("bull" . 2) ("mills" . 3) ("mall" . 3) ("miles" . 3) ("smile" . 3) ("silly" . 3) ("shill" . 3) ("smiles" . 4) ("hilly" . 4))
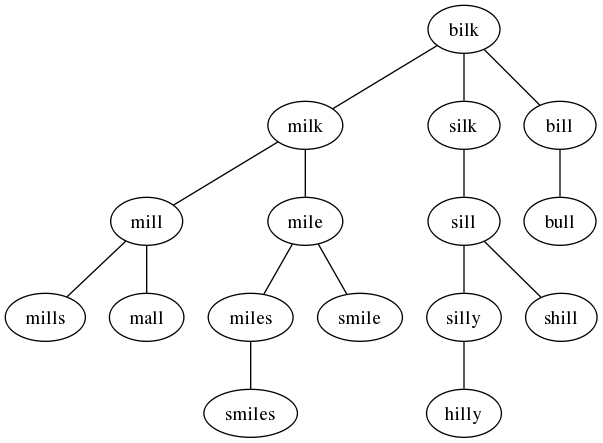
Thus “milk” is a direct friend of “bilk” and “mills” is a friend of a friend of a friend.
We can see the network more clearly by specifying graph as t. That causes social to call sgraph to output a dot program to produce a graph. Here’s sgraph:
(defun sgraph (edges) "Output a dot program for the social graph of word in words." (with-output-to-string (stream) (format stream "graph G { ~%") (mapc (lambda (e) (format stream "~a -- ~a~%" (car e) (cdr e))) edges) (format stream "}~%")))
For our example, this produces the program
graph G {
bilk -- milk
bilk -- silk
bilk -- bill
milk -- mill
milk -- mile
silk -- sill
bill -- bull
mill -- mills
mill -- mall
mile -- miles
mile -- smile
sill -- silly
sill -- shill
miles -- smiles
silly -- hilly
}
which produces the graph